線形部分空間であることを示せ ベクトル
W x R 2 1 2 2 1 x 1 x 2 0 0 W x R 2 1 2 2 1 x 1 x 2 0 0 問題の意味を解説. X 2 y 2 z 2 1.

線形変換の示し方 写真の 2 が回答で明らかなので省略するとなっていて Okwave

ベクトル空間の基本定理3 部分空間の次元に関する定理への応用 身勝手な主張

線形独立であれば1組の基底となる と言える理由 Okwave
2 V 8.
線形部分空間であることを示せ ベクトル. 1 V 8. 明らかに満たすので vec0 in W_1 である. となることである ベクトル空間部分ベクトル空間の定義と具体例10個 まず全射について証明しよう boldsymboly_1 boldsymboly_2 in operatornameIm f とする定義よりある boldsymbolv_1 boldsymbolv_2 in V が存在して.
線形数学II 演習問題 第1回 ベクトル空間部分空間 1. 3 M 3. 各項が実数であるような数列全体のなすベクトル空間S 例15 参照 に対して Sc ajg 1 j0 2 S fa jg は収束converge する とおくとSc はS の部分空間である 3 前期はとくにV Rn の場合を考えたが一般のベクトル空間でも同じ.
次の W W はベクトル空間 R 2 R 2 の部分空間かどうか調べよ. クトル空間であることを示せさらにn 3のときこの部分ベクトル空間を図示 せよ 2 nを自然数とするRxの元で次数が高々dであるようなもの全体をPd と書くPd はRxの部分ベクトル空間であることを示せ 3 問題23のベクトル空間は同問題1の. 以下で与えられるR3 の部分集合V がR3 の加法とスカラー倍でR3 の部分空間であるかどうかを 理由ととも に答えよ.
部分空間をやっているのですが意味不明ですなにがやりたいのか全くわかりませんWAxxRnこれが何を意味しているのかもわかりませんわかる方色々と詳しく教えていただけ たらうれしいです 線形空間はほとんどの人にとって空間とよばれるものに接する初めての機会. ベクトル空間 定義ベクトル空間 集合 が次ページのv 和の公理および スカラー倍の公理 を満たすと 集合 をv 線形空間 または ベクトル空間 という 数学では空間は集合の別名で用いられる 特にある特定の性質を満たす集合として 16. 演習問題36 3 次元のベクトル空間上で次のように集合W を定義する W fxyz0 j x-2y3z 0g W が部分空間であることを示せ.
0 B x y z 1 C A2 R3 xy 0 9. の3つをすべて示す必要があります 逆にa b cのうち1つでも満たさないものがあれば部分空間とはいえません 1 a 原点において式を満たすか. 2 M 2.
4 M 4. ル空間K C のときn 次元複素数ベクトル空間と呼ぶ次元の定義 13 例2. Vがベクトル空間でw1w2がvの部分空間のときw1 w2もvの部分空間であることを示せはキャップuの逆ですどうしても分かりませんお願いします定義は判っていますか線型空間 v の部分集合 w が v の部分線型空間であるとは.
設問1WλxAxλxがR2の部分空間となることを示せ 上記は固有値を求めたあと具体例があると嬉しい設問2fxY線形写像とするkerfimfのどちらかについてベクトル空間となることを示せこれらについてご教授していただきたいですどちらも具体例を挙げて示してほしいです何卒. MmnK K を成分にもつmn 行列全体 は行列の和とスカラー積に関してK 上のベクトル空間となるこれらはベクトル空間と してはKmn と同型ベクトル空間の同型 31 であるがlm. 5 M 5.
ベクトル 空間 部分 空間
2
大学数学の線形代数の ベクトル空間の問題です を付けた1 2 1 Yahoo 知恵袋

数学 10回目
2

入門線形代数 部分空間 ベクトル空間 大学ますまとめ
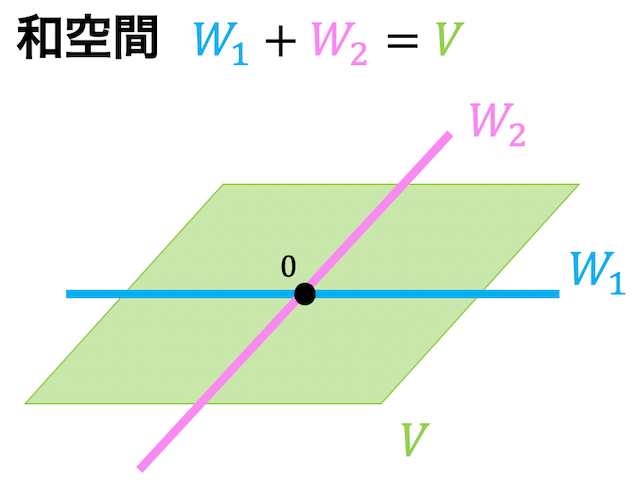
うさぎでもわかる線形代数 第09羽 部分空間その2 和空間 交空間 工業大学生ももやまのうさぎ塾

線形の問題をやりました 模範解答はないんですが一部でもいいのであってますか Clearnote
You have just read the article entitled 線形部分空間であることを示せ ベクトル. You can also bookmark this page with the URL : https://jamesonzasqy.blogspot.com/2022/10/blog-post_574.html

0 Response to "線形部分空間であることを示せ ベクトル"
Post a Comment